Answer:
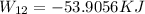
Part A:
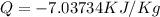 (-ve sign shows heat is getting out)
(-ve sign shows heat is getting out)
Part B:
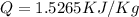 (Heat getting in)
(Heat getting in)
The value of Q at constant specific heat is approximately 361% in difference with variable specific heat and at constant specific heat Q has opposite direction (going in) than Q which is calculated in Part B from table A-23. So taking constant specific heat is not a good idea and is questionable.
Step-by-step explanation:
Assumptions:
- Gas is ideal
- System is closed system.
- K.E and P.E is neglected
- Process is polytropic
Since Process is polytropic so
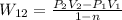
Where n=1.25
Since Process is polytropic :
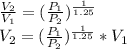
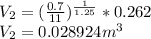
Now,
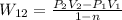
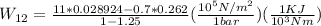
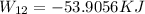
We will now calculate mass (m) and Temperature T_2.
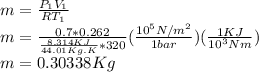
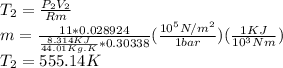
Part A:
According to energy balance::
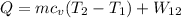
From A-20, C_v for Carbon dioxide at 300 K is 0.657 KJ/Kg.k
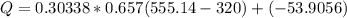
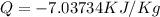 (-ve sign shows heat is getting out)
(-ve sign shows heat is getting out)
Part B:
From Table A-23:
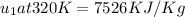
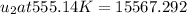 (By interpolation)
(By interpolation)
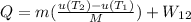
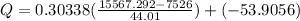
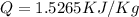 (Heat getting in)
(Heat getting in)
The value of Q at constant specific heat is approximately 361% in difference with variable specific heat and at constant specific heat Q has opposite direction (going in) than Q which is calculated in Part B from table A-23. So taking constant specific heat is not a good idea and is questionable.