Question

Suppose the object moving is Dave, who hasamassofmo =66kgatrest. Whatis Daveâs mass at 90% of the speed of light? At 99% of the speed of light? At 99.9% of the speed of light? and How fast should Dave be moving to have a mass of 500 kg?

Answer 1

Explanation:

Formula that relates the mass of an object at rest and its mass when it is moving at a speed v:

`m=\frac{m_o}{\sqrt{1-(v^2)/(c^2)}}`

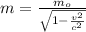
Where :

m = mass of the oebjct in motion

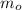`m_o` = mass of the object when at rest

v = velocity of a moving object

c = speed of the light =
`3* 0^8 m/s`

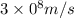
We have :

1) Mass of the Dave =
`m_o=66 kg`

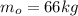
Velocity of Dave ,v= 90% of speed of light = 0.90c

Mass of the Dave when moving at 90% of the speed of light:

`m=\frac{66 kg}{\sqrt{1-((0.90c)^2)/(c^2)}}`

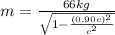
m = 151.41 kg

Mass of Dave when when moving at 90% of the speed of light is 151.41 kg.

2) Velocity of Dave ,v= 99% of speed of light = 0.99c

Mass of the Dave when moving at 99% of the speed of light:

`m=\frac{66 kg}{\sqrt{1-((0.99c)^2)/(c^2)}}`

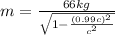
m = 467.86 kg

Mass of Dave when when moving at 99% of the speed of light is 467.86 kg.

3) Velocity of Dave ,v= 99.9% of speed of light = 0.999c

Mass of the Dave when moving at 99.9% of the speed of light:

`m=\frac{66 kg}{\sqrt{1-((0.999c)^2)/(c^2)}}`

m = 1,467.17 kg

Mass of Dave when when moving at 99.9% of the speed of light is 1,467.17 kg.

4) Mass of the Dave =
`m_o=66 kg`

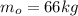
Velocity of Dave,v=?

Mass of the Dave when moving at v speed of light: 500

`500 kg=\frac{66 kg}{\sqrt{1-((v)^2)/((3* 10^8 m/s)^2)}}`

`v=2.973* 10^8 m/s`

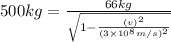
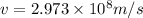
Dave should be moving at speed of
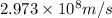`2.973* 10^8 m/s`.