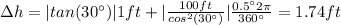Question

A right triangle has base b = 100 plusminus 1 ft and adjacent angle theta = 30 degree plusminus 0.5 degree. Calculate the height h and its uncertainty.

Answer 1

The height h of this right triangle is 57.74±1.74ft.

Step-by-step explanation:

Knowing that this is a right triangle, if one of the angles adjacent to the base, θ is 30º, the other angle is 90º. Therefore we can calculate the height h can be calculated with the tangent:

`tan(\theta)=(h)/(b)\leftrightarrow h=tan(\theta)b=tan(30^\circ)100ft=57.74ft`

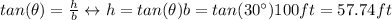
For the uncertainty we use the partial derivatives:

`\Delta h=|(dh)/(db)|\Delta b+ |(dh)/(d\theta)|\Delta \theta\\\Delta h=|tan(\theta)|\Delta b+ |(b)/(cos^2(\theta))|\Delta \theta`

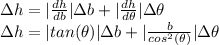
We have to be careful to use Δθ in radians:

`\Delta h=|tan(30^\circ)|1ft+ |(100ft)/(cos^2(30^\circ))|(0.5^\circ2\pi)/(360^\circ)=1.74ft`