Answer:
b) 95%
Explanation:
We have been given that scores on an approximately bell shaped distribution with a mean of 76.4 and a standard deviation of 6.1 points. We are asked to find the percentage of the data that is between 64.2 points and 88.6 points.
First of all, we will find z-scores of each data point as:

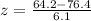

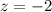
Let us find z-score corresponding to normal score 88.6.


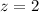
To find the percentage of the data is between 64.2 points and 88.6 points, we need to find area under a normal distribution curve that lie within two standard deviation of mean.
The empirical rule of normal distribution states that approximately 95% of data points fall within two standard deviation of mean, therefore, option 'b' is the correct choice.