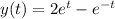Question

In this problem, y = c1ex + c2eâx is a two-parameter family of solutions of the second-order DE y'' â y = 0. Find a solution of the second-order IVP consisting of this differential equation and the given initial conditions. y(â1) = 3, y'(â1) = â3

Answer 1

`y(t) = 2e^t -e^(-t)`

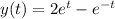
Explanation:

Assuming this complete problem: "In this problem,

y = c1ex + c2e−x

is a two-parameter family of solutions of the second-order DE

y'' − y = 0.

Find a solution of the second-order IVP consisting of this differential equation and the given initial conditions.

y(0) = 1, y'(0)= 3"

Solution to the problem

For this case we have a homogenous, linear differential equation with order 2, and with the general form:

`ay'' +by' +cy=0`

Where
`a =1, b=0, c=-1`

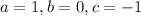
And we can rewrite the differential equation in terms
`y = e^(rt)` like this:

`[e^(rt)]'' -e^(rt)=0`

And applying the second derivate we got:

`r^2 e^(rt) -e^(rt)=0`

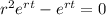
We can take common factor
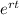`e^(rt)` and we got:

`e^(rt) (r^2-1) =0`

And for this case the two only possibel solutions are
`r=1, r=-1`

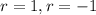
And the general solution for this case is given by:

`y = c_1 e^(r_1 t) + c_2 e^(r_2 t)`

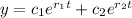
Replacing the roots that we found we got:

`y = c_1 e^(t) +c_2 e^(-t)`

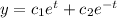
Now we can find the derivates for this last espression

`y' = c_1 e^t -c_2 e^(-t)`

`y'' = c_1 e^t +c_2 e^(-t)`

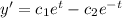
From the initial conditions we have this:

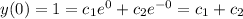`y(0)=1 =c_1 e^(0) +c_2 e^(-0)= c_1 +c_2` (1)

`y'(0) =3= c_1 e^(0) -c_2e^(-0)= c_1 -c_2` (2)

If we add equations (1) and (2) we got:

`4 = 2c_1 , c_1 = 2`

And solving for
`c_2` we got:

`c_2=3-c_1= 3-2 = 1`

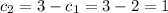
So then our general solution is given by:

`y(t) = 2e^t -e^(-t)`