Answer:
x =
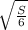 or
or

Step-by-step explanation:
The cardboard box is in the shape of a cube. The surface area of the box is given by:
S = 6

To find the inverse, we have to solve for x. To solve for x means we will make x the subject of the equation above
Divide both the right and left hand side by 6, we have:
6
 ÷ 6 = S ÷ 6 ⇒
÷ 6 = S ÷ 6 ⇒
 =
=
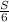
 =
=
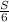
Take the square root for both the right and left hand side, we have:
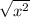 =
=
 ⇒ x =
⇒ x =

x =
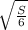 or
or

Therefore, x is equivalent to the square root of (S/6)