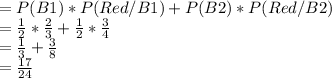Answer:
\frac{17}{24}
Explanation:
Given that Box 1 contains 2 red balls and 1 blue ball. Box 2 contains 3 blue balls and 1 red ball. A coin is tossed. If it falls heads up, box 1 is selected and a ball is drawn. If it falls tails up, box 2 is selected and a ball is drawn.
P(selecting Box 1) = 0.5 = P(selecting II box) (assuming a fair coin is tossed)
P(Red/Box I ) =
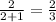
P(Red/Box II) =
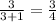
Box 1 and Box 2 are mutually exclusive and exhaustive events.
So probability of selecting a red ball.
= probability of selecting a red ball from box 1 + probability of selecting a red ball frm box 2