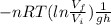Answer:
A) m =
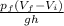
B) m =
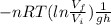
Step-by-step explanation:
A) a process at the constant external pressure Pf,
We Know that
W = mgh-------------------------(1)
W=
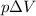 ---------------------------(2)
---------------------------(2)
Equating (1) and(2)
mgh =
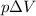
=
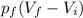
Therefore m =
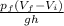
B)In a irreversible process
W = mgh----------------------(3)
 ---------------------(4)
---------------------(4)
PV =nRT
P =


W =
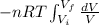
W=

W=
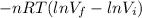
W=

From EQ(3)
mgh=

m =