Question

Determine the dimensions of the derivative dx/dt = 3At^2 + B. (Use the following as necessary: L and T, where L is the unit of length and T is the unit of time.)[dx/dt] = ___?

Answer 1

LT⁻¹

Step-by-step explanation:

Assuming the given expression is

x = A t³ + B t.........(1)

x is the distance

we have to calculate dimension of dx/dt

from expression (1)

x = A t³

`A = (L)/(T^3)`

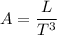
A = LT⁻³

x = B t

B = LT⁻¹

now,

dx/dt = 3At^2 + B

from rule of dimension

dimension of dx/dt is equal to dimension of At^2

dx/dt = A t²

dx/dt = LT⁻³ x T²

dx/dt = LT⁻¹

hence, dimension of dx/dt is equal to LT⁻¹