Question

For the electromagnetic field described by the equations below, show (a) under what conditions of ω and k does the field satisfy Maxwell’s equations? And (b), suppose that ω = 1010 s−1 and E0 = 10 kV/m. What is the wavelength? What is the energy density in joules per cubic meter, averaged over a large region? From this calculate the power density, the energy flow in joules per square meter per second.

Answer 1

The electromagnetic field satisfies Maxwell's equations when ω and k correspond to the light speed relationship ω = c*k. With ω = 10^10 s^-1 and E0 = 10 kV/m, the wavelength and energy density can be calculated, and the Poynting vector gives the power density of the wave.

Step-by-step explanation:

Conditions for Satisfying Maxwell's Equations and Power Density Calculation

The electromagnetic field described above will satisfy Maxwell's equations if the frequency ω and wavenumber k are related by the equation ω = c*k, where c is the speed of light in vacuum. Given that ω = 1010 s-1 and the amplitude for the electric field E0 = 10 kV/m, we calculate the wavelength, λ, using λ = 2π/k or λ = c/ω.

The energy density u of an electromagnetic wave is given by the sum of the energy densities of the electric and magnetic fields, so u = (ε₀E₀²/2) + (B₀²/2μ₀), where ε₀ is the permittivity of free space and μ₀ is the permeability of free space. The power density, or intensity of the wave, is given by the Poynting vector, S = u*c, which indicates the energy flow per unit area per unit time.

Answer 2

a) w / k = c , b) λ = 1,887 10⁻¹ m ,
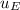`u_(E)` = 4.42 10⁻⁴ J / m³

Step-by-step explanation:

a) Maxwell's equations when solved for an electromagnetic wave result in

E = E₀ cos (kx - wt)

B = B₀ cos (kx -wt)

Where k is the vector ce wave and w the angular velocity

k = 2π / λ

w = 2π f

Let's divide the two equations

w / k = f λ

w / k = c

Therefore, for w and k to be a solution to Maxwell's equations, their relationship must be equal to the speed of light.

b) If w = 10¹⁰ s⁻¹

w = 2π f

f = w / 2π

f = 10¹⁰ / 2π

f = 1.59 10⁹ Hz

The speed of light is

c = λ f

λ = c / f

λ = 3 10⁸ / 1.59 10⁹

λ = 1,887 10⁻¹ m

Energy density is

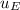`u_(E)` = ½ ε₀ E₀²

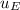`u_(E)` = ½ 8.85 10⁻¹² (10 10³)²

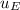`u_(E)` = 4.42 10⁻⁴ J / m³

Power is energy per unit of time

P =
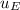`u_(E)` / t

We calculate for every second

P = 4.42 10⁻⁴ W / m³

The flow or intensity of energy is

I = S = c u

I = 3. 108 4.42 10⁻⁴

I = 1.33 10⁵ W / m2