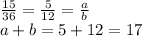Question

Dawn and abed each roll a standard die obtaining a random number from 1 to 6. if the probability that dawns number is larger than abeds number can be expressed by a/b in simplest form, compute a + b.

Answer 1

a+b = 12

Explanation:

There are 36 possible outcomes for rolling two dice. Let A be the number rolled by Abed and D be the number rolled by Dawn. The sample space, in the format [A,D], of all of the possibilities in which Dawn's number is larger is:

[5,6]

[4,5] [4,6]

[3.4] [3,5] [3.6]

[2,3] [2.4] [2,5] [2.6]

[1,2] [1,3] [1.4] [1,5] [1.6]

There are 15 ways out of 36 possible ways of Dawn getting the higher number. In the simplest form:

`(15)/(36)=(5)/(12)=(a)/(b)\\ a+b = 5+12 = 17`