Answer: The percentage abundance of
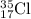 and
and
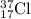 isotopes are 77.5% and 22.5% respectively.
isotopes are 77.5% and 22.5% respectively.
Step-by-step explanation:
Average atomic mass of an element is defined as the sum of masses of each isotope each multiplied by their natural fractional abundance.
Formula used to calculate average atomic mass follows:
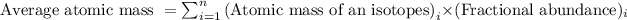 .....(1)
.....(1)
Let the fractional abundance of
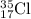 isotope be 'x'. So, fractional abundance of
isotope be 'x'. So, fractional abundance of
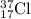 isotope will be '1 - x'
isotope will be '1 - x'
- For
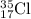 isotope:
isotope:
Mass of
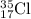 isotope = 35 amu
isotope = 35 amu
Fractional abundance of
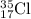 isotope = x
isotope = x
- For
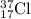 isotope:
isotope:
Mass of
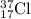 isotope = 37 amu
isotope = 37 amu
Fractional abundance of
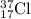 isotope = 1 - x
isotope = 1 - x
Average atomic mass of chlorine = 35.45 amu
Putting values in equation 1, we get:
![35.45=[(35* x)+(37* (1-x))]\\\\x=0.775](https://img.qammunity.org/2021/formulas/chemistry/high-school/s3xz54aex3agifagm4ouekcyc4xr35rak3.png)
Percentage abundance of
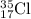 isotope =
isotope =
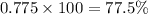
Percentage abundance of
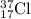 isotope =
isotope =
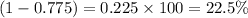
Hence, the percentage abundance of
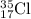 and
and
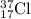 isotopes are 77.5% and 22.5% respectively.
isotopes are 77.5% and 22.5% respectively.