Question

A Porsche 944 Turbo has a rated engine power of 217hp . 30% of the power is lost in the drive train, and 70% reaches the wheels. The total mass of the car and driver is 1520 kg, and two-thirds of the weight is over the drive wheels.

a) What is the maximum acceleration of the Porsche on a concrete surface where μs=1?

b) What is the speed of the Porsche at maximum power output?

c) If the Porsche accelerates at amax , how long does it take until it reaches the maximum power output?

Answer 1

Step-by-step explanation:

(a) It is given that two-third of weight is over the drive wheels. So, mathematically, w =
`(2)/(3)mg`.

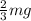Hence, maximum force is expressed as follows.

`F_(max) = \mu_(s) * w`

`m * a_(max) = \mu_(s) ((2)/(3) mg)`

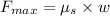
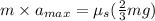
Hence, the maximum acceleration is calculated as follows.

`a_(max) = (2)/(3) \mu_(s) * g`

=
`(2)/(3) * 1.00 * 9.8 m/s^(2)`

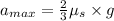
= 6.53
`m/s^(2)`

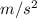
Hence, the maximum acceleration of the Porsche on a concrete surface where μs = 1 is 6.53
`m/s^(2)`.

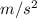(b) Since, 30% of the power is lost in the drive train. So, the new power is 70% of
`P_(max)`.

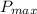That is, new power =
`0.7 * P_(max)`

Now, the expression for power in terms of force and velocity is as follows.

P =
`F_(max) \\u`

`0.7 P_(max) = ma_(max) \\u`

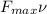
Therefore, speed of the Porsche at maximum power output is as follows.

`\\u = 0.7 * (P_(max))/(ma_(max))`

=
`0.7 * (217 hp * (746 W)/(1 hp))/(1500 kg * 6.53 m/s^(2))`

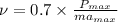
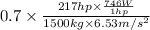
= 11.568 m/s

= 11.57 m/s

Therefore, speed of the Porsche at maximum power output is 11.57 m/s.

(c) The time taken will be calculated as follows.

time =
`\frac{\text{velocity}}{\text{acceleration}}`

=
`(11.57 m/s)/(6.53 m/s^(2))`

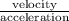
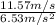
= 1.77 s

Therefore, the Porsche takes 1.77 sec until it reaches the maximum power output.