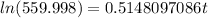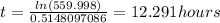Answer:
1)
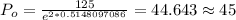
2)
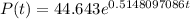
3)
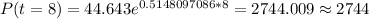
4)
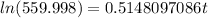
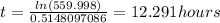
Explanation:
The exponential model on this case is given by the following formula:
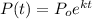
Where P represent the population, k the growth/decay constant and t the time in hours for this case.
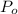 represent the initial population
represent the initial population
We have some initial conditions given:
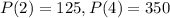
Part 1
From the initial conditions we have the following equations:
 (1)
(1)
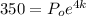 (2)
(2)
We can solve for
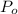 from equation (1) like this:
from equation (1) like this:
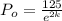
And we can replace this into equation (2) and we got:
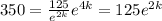
And we can divide both sides by 125:

Now we can apply natural log on both sides and we got:

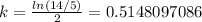
And now since we have the value of k we can solve for
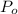 like this:
like this:
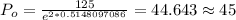
Part 2
For this case the exponential model is given by:
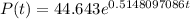
Part 3
For this case we just need to replace t=8 and see what we got:
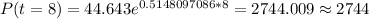
Part 4
For this case we want to solve this:
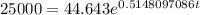
We can divide both sides by 44.643 and we got:
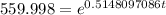
Now we can apply natural logs on both sides: