Answer:
a) H0:
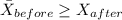
H1:
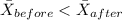
Or equivalently:
H0:
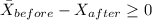
H1:
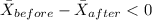
b) The hypothesis test can tell to us if the difference is significantly at some confidence level selected. And that's more important than just the simple difference obtained between 75-65= 10%, because when we do inference we are analyzing the population of interest and not just the sample. And if our conclusion for the test is that the null hypothesis is rejected we can conclude that we have an improvement on the scores for the population at some significance level.
c) The p value is a measure of probability in order to compare with a significance level provided if we can reject or not the null hypothesis.
For this case the p value since is a left tailed test would be given by:
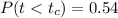
And using any significance level
 we fail to reject the null hypothesis because
we fail to reject the null hypothesis because
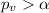 . And on that case we can't conclude that the scores after are significantly better than before.
. And on that case we can't conclude that the scores after are significantly better than before.
Explanation:
Part a
For this case we have this information given:
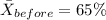
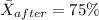
For this case the most appropiate system of hypothesis would be:
H0:
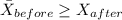
H1:
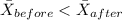
Or equivalently:
H0:
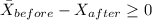
H1:
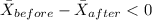
Part b
The hypothesis test can tell to us if the difference is significantly at some confidence level selected. And that's more important than just the simple difference obtained between 75-65= 10%, because when we do inference we are analyzing the population of interest and not just the sample. And if our conclusion for the test is that the null hypothesis is rejected we can conclude that we have an improvement on the scores for the population at some significance level.
Part c
The p value is a measure of probability in order to compare with a significance level provided if we can reject or not the null hypothesis.
For this case the p value since is a left tailed test would be given by:
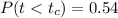
And using any significance level
 we fail to reject the null hypothesis because
we fail to reject the null hypothesis because
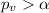 . And on that case we can't conclude that the scores after are significantly better than before.
. And on that case we can't conclude that the scores after are significantly better than before.