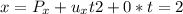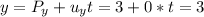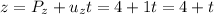Question

find a set of parametric equations of the line the line pases through the point (2,3,4) and is parallel to the xz-plane and the yz-plane.

Answer 1

`x=2, y=3, z=4+t`

Explanation:

For this case we need a line parallel to the plane x z and yz. And by definition of parallel we see that the intersection between the xz and yz plane is the z axis. And we can take the following unitary vector to construct the parametric equations:

`u= (u_x, u_y, u_z)= (0,0,1)`

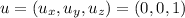
Or any factor of u but for simplicity let's take the unitary vector.

Then the parametric equations are given by:

`x= P_x + u_x t`

`y= P_y + u_y t`

`z= P_z + u_z t`

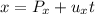
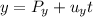
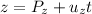
Where the point given
`P=(2,3,4)= (P_x , P_y, P_z)`

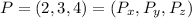
And then since we have everything we can replace like this:

`x= P_x + u_x t 2+ 0*t = 2`

`y= P_y + u_y t= 3+ 0*t = 3`

`z= P_z + u_z t = 4+ 1t = 4+t`

`x=2, y=3, z=4+t`