Question

The director of research and development is testing a new medicine. She wants to know if there is evidence at the 0.05 level that the medicine relieves pain in more than 325 seconds.

After performing a hypothesis test, she decides to reject the null hypothesis. What is the conclusion?

a. There is sufficient evidence at the 0.05 level of significance that the medicine relieves pain in more than 325 seconds.

b. There is not sufficient evidence at the 0.05 level of significance that the medicine relieves pain in more than 325 seconds.

Answer 1

a. There is sufficient evidence at the 0.05 level of significance that the medicine relieves pain in more than 325 seconds.

Explanation:

With the info provided let the parameter of interest
`\mu` who represent the mean that the medicine relieves pain, the system of hypothesis would be:

Null Hyp:
`\mu \leq 325`

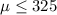
Alternative Hyp :
`\mu >325`

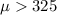
If we know the population deviation, is better apply a z test to compare the actual mean to the reference value, and the statistic is given by:

`z=(\bar X-\mu_o)/((\sigma)/(√(n)))`

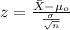
z-test: "Is used to compare group means. Is one of the most common tests and is used to determine if the mean is (higher, less or not equal) to an specified value".

If the deviation is not known we can use the t test with the following statistic:

`t=(\bar X-\mu_o)/((s)/(√(n)))`

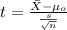
On this case the decision was REJECT the null hypothesis. That means that we obtain a significant result with a p value lower than the signficance level

`p_v <\alpha=0.05`

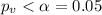
So then we can conclude this:

a. There is sufficient evidence at the 0.05 level of significance that the medicine relieves pain in more than 325 seconds.