Question

What does the fundamental theorem of algebra and its corollary tell you about the roots of the polynomial equation p(x)=0 where p(x) has degree n?

Answer 1

A polynomial with complex coefficients of degree n has n complex roots, counted with multiplicity.

Explanation:

We are given a polynomial p(x) in the question with degree n.

The degree n means the n is the highest power of variable in the given polynomial.

The equation:

`p(x) = 0`

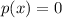
Fundamental theorem of Algebra

• The Fundamental theorem of Algebra states that a a polynomial of degree n will have n roots of the equation.

This can further be explained as:

• A polynomial with complex coefficients of degree n has n complex roots, counted with multiplicity.