Answer:
Option A) f(n)=-5-4n is correct.
The equation would produce the same sequence of numbers as the recursive formula is f(n)=-5-4n
Explanation:
Given that a=-9 and

The recursive formula is

Therefore d=-4
Let
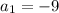 and d=-4
and d=-4
We can find
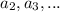
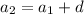
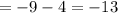
Therefore
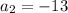

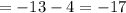
Therefore
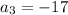 and so on.
and so on.
Therefore the arithmetic sequence is
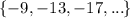
Option A) f(n)=-5-4n is correct.
f(n)=-5-4n
put n=1 in f(n)=-5-4n
f(1)=-5-4(1)
=-9
Therefore f(1)=-9
put n=2 in f(n)=-5-4n
f(21)=-5-4(2)
=-5-8
Therefore f(2)=-13
put n=3 we get f(n)=-5-4n
f(3)=-5-4(3)
=-5-12
Therefore f(3)=-17 and so on .
Therefore the sequence is
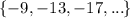
Therefore the equation would produce the same sequence of numbers as the recursive formula is f(n)=-5-4n