Question

An object attached to a spring is pulled down a distance of 3 inches below the point of equilibrium. It completes one oscillation in 2 seconds. Find the equation of the motion, when will it have covered a distance of 9 inches.

Answer 1

`x(t = 1.5) = 3\cos(3\pi/2) = 9`

Step-by-step explanation:

The equation of motion in simple harmonic motion is

`x(t) = A\cos(\omega t +\phi)`

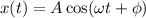
where Ф is the phase angle to be determined by the initial conditions.

At t = 0, the object is pulled 3 inches, which means A = 3.

If the object completes one oscillation in 2 sec. then its period is 2 sec, T = 2.

`\omega = (2\pi)/(T) = (2\pi)/(2) = \pi`

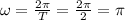
The phase angle can now be determined.

`x(t = 0) = A\cos(0 + \phi) = A\cos(\phi)\\3 = 3\cos(\phi)\\cos(\phi) = 1\\\phi = 0`

So, the general equation of motion is

`x(t) = 3\cos(\pi t)`

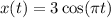
When it will have covered a distance of 9 inches, it is at the equilibrium position. From A to 0, from 0 to -A, then from -A to 0 again to complete 9 inches, since A = 3.

`0 = 3\cos(\pi t)\\\cos(\pi t) = 0\\\phi = \pi/2~{\rm or}~3\pi/2\\t = 0.5s~ {\rm or} ~1.5s`

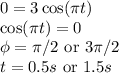
Since we know that a full oscillation is completed in 2 sec. than 3/4 oscillation should be completed in 1.5s.

So, equation of motion at that instant is

`x(t = 1.5) = 3\cos(3\pi/2) = 9`