Question

PLEASE HELP!

Carl drew a rectangle with a width of 8 in. and a length of 32 in. Which rectangles are NOT similar to Carl's rectangle? Select ALL that apply.

a. a rectangle with a width of 23cm and a length of 92cm

b. a rectangle with a width of 2.5in and a length of 10in

c. a rectangle with a width of 9mm and length of 45mm

d. a rectangle with a width of 10 cm and a length of 44 cm

Answer 1

c) A rectangle with width of 9 mm and length of 45 cm.

d) A rectangle with width of 10 cm and length of 44 cm.

Explanation:

Given:

Length of the rectangle = 32 in.

Width of the rectangle = 8 in.

First we will find the ratio of length by width.

`(length)/(width)= (32)/(8) = (4)/(1) \ \ \ \ equation \ 1`

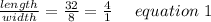
Now we need to find from the given Option which rectangles are not similar to Carl's Rectangle.

So we will check for each.

a) A rectangle with width of 23 cm and length of 92 cm.

we will find the ratio of length by width.

`(length)/(width)= (92)/(23) = (4)/(1) \ \ \ \ equation \ 2`

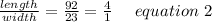
By Definition of Similar rectangles which states that;

"When ratio of the dimension of 2 corresponding rectangles are equal then the 2 rectangles are said to be similar."

Now Comparing equation 1 and equation 2 we get;

equation 1
`=` equation 2

Hence This rectangle is similar to Carl's rectangle.

b) A rectangle with width of 2.5 inch and length of 10 inch.

we will find the ratio of length by width.

`(length)/(width)= (10)/(2.5) = (4)/(1) \ \ \ \ equation \ 2`

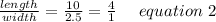
By Definition of Similar rectangles which states that;

"When ratio of the dimension of 2 corresponding rectangles are equal then the 2 rectangles are said to be similar."

Now Comparing equation 1 and equation 2 we get;

equation 1
`=` equation 2

Hence This rectangle is similar to Carl's rectangle.

c) A rectangle with width of 9 mm and length of 45 cm.

we will find the ratio of length by width.

`(length)/(width)= (45)/(9) = (5)/(1) \ \ \ \ equation \ 2`

By Definition of Similar rectangles which states that;

"When ratio of the dimension of corresponding rectangles are equal then the 2 rectangles are said to be similar."

Now Comparing equation 1 and equation 2 we get;

equation 1
`\\eq` equation 2

Hence This rectangle is not similar to Carl's rectangle.

d) A rectangle with width of 10 cm and length of 44 cm.

we will find the ratio of length by width.

`(length)/(width)= (44)/(10) = (11)/(5) \ \ \ \ equation \ 2`

By Definition of Similar rectangles which states that;

"When ratio of the dimension of corresponding rectangles are equal then the 2 rectangles are said to be similar."

Now Comparing equation 1 and equation 2 we get;

equation 1
`\\eq` equation 2

Hence This rectangle is not similar to Carl's rectangle.