Question

An electron moving along the x axis has a position given by x = 16.0 te-t m, where t is in seconds. How far is the electron from the origin when it momentarily stops?

Answer 1

The electron is 5.88 m far from origin when it momentarily stops.

Step-by-step explanation:

The position of electron on x-axis is given by the equation:

x = 16 t
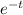`e^(-t)` m __________ eqn(1)

The speed of particle can be found out by taking derivative of "x" with respect to "t"

V = dx/dt = 16[-t
`e^(-t)` +
`e^(-t)`]

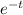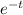V = 16
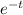`e^(-t)`(1 - t)

Now, when the electron stops, its velocity becomes zero.

V = 0 = 16
`e^(-t)`(1 - t)

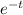`e^(-t)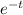`(1 - t) = 0

Either:
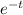`e^(-t)` = 0

-t = ln(0)

t = infinity (Since, time can not be infinite, thus this answer is rejected)

Or: 1 - t = 0

t = 1 sec

Therefore, at t= 1 sec, the electron will stop momentarily.

Using t = 1 sec in eqn (1), we find the position of electron.

x = 16(1)
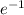`e^(-1)` m

x = 5.88 m