Question

Find the distance between the points given. (-10, 3) and (-10, 12) √(17) 9 15

Answer 1

The Third option is correct 9 .

Therefore the distance between the points given. (-10, 3) and (-10, 12) is

9 units.

Explanation:

Given:

Consider,

point A( x₁ , y₁) ≡ ( -2 ,-2 )

point B( x₂ , y₂) ≡ ( 4 , -10 )

To Find:

Distance between AB = ?

Solution:

Distance Formula between Two point is given as

`l(AB) = \sqrt{((x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2) )}`

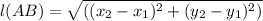
Substituting the values we get

`l(AB) = \sqrt{((-10-(-10))^(2)+(12-3)^(2) )}`

`l(AB) = \sqrt{((-10+10))^(2)+(9)^(2) )}`

`l(AB) = \sqrt{(0)^(2)+81}\\l(AB)=√(81)=9\\l(AB)=9\ unit`

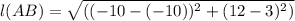
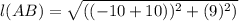
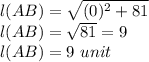
Therefore the distance between the points given. (-10, 3) and (-10, 12) is

9 units.