Question

The passengers in a roller coaster car feel 50% heavier than their true weight as the car goes through a dip with a 20 m radius of curvature.What is the car's speed at the bottom of the dip?

Answer 1

Step-by-step explanation:

Force = weight + 50% of weight = 1.5 mg

Weight = mg

Let v be the speed.

radius, r = 20 m

According to the Newtons second law

F = mg + mv²/r

1.5 mg = mg + mv²/r

0.5 g = v²/r

v² = 0.5 x 9.8 x 20

v = 9.8 m/s

Answer 2

v= 10 m/s

Step-by-step explanation:

Given that

Radius ,r= 20 m

The total wight R

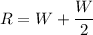`R=W+(W)/(2)` ( 50% heavier)

Lets take ,mass = m kg

`R=mg+(mg)/(2)`

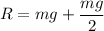
Now by applying Newton's Second law

Total Force
`F= mg+(mv^2)/(r)`

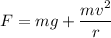
v=speed of the car at the bottom

Now by balancing the above forces

`mg+(mg)/(2)= mg+(mv^2)/(r)`

`(mg)/(2)= (mv^2)/(r)`

`(g)/(2)= (v^2)/(r)`

`v=\sqrt{(gr)/(2)}`

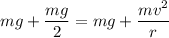
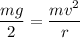
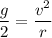
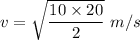`v=\sqrt{(10* 20)/(2)}\ m/s` ( take g= 10 m/s²)

v= 10 m/s