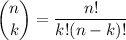There are
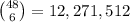 ways of drawing 6 numbers between 1 and 48.
ways of drawing 6 numbers between 1 and 48.
Of the 6 drawn numbers, there are
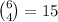 ways of drawing 4 matching numbers, and
ways of drawing 4 matching numbers, and
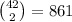 ways of drawing any 2 non-matching numbers.
ways of drawing any 2 non-matching numbers.
Hence the probability of winning the prize is
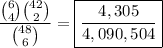
Note: In case you're unfamiliar with the notation,