Question

How far away from the tree is the girl ?

A. 30 feet
B. 70 feet
C. 20 feet
D. 50 feet

Answer 1

The correct option is C. 50 feet.

Therefore the girl is 50 feet away from the tree.

Explanation:

Consider a Right angle Triangle

Elevation to the tree is ' θ '

Adjacent Side to θ = distance from the tree to girl = distance

Opposite Side to θ = height of the tree = height

`\tan \theta =(20)/(50)`

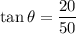
To Find:

distance from the tree to girl = distance

Solution:

In Right angle Triangle Tangent Identity

`\tan \theta = \frac{\textrm{side opposite to angle theta}}{\textrm{side adjacent to angle theta}}`

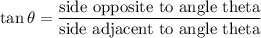
Substituting we get

`\tan \theta = \frac{\textrm{height of the tree}}{\textrm{distance from the tree to girl}}`

`\tan \theta = (height)/(distance)`

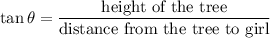
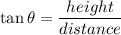
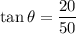`\tan \theta =(20)/(50)` ........Given

Comparing the given equation with the above we get

`distance =50\ feet`

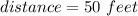
Therefore the girl is 50 feet away from the tree.