Answer:
(a) Decrease
(b) Will remain same
(c) Increase
(d) Time period will be infinite
Step-by-step explanation:
Time period of simple pendulum is given as
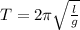
From he expression we can see that time period is inversely proportional to the acceleration due to gravity
(a) Upward acceleration is
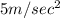
So
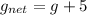
As the acceleration due to gravity increases so time period will decrease
(b) Moves upward with at a steady 5 m /sec
So
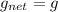
So time period will be same
(c) Downward acceleration is
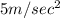
So
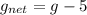
As the acceleration due to gravity decreases so time period will increase
(d) Downward acceleration is
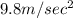
So
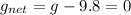
As the acceleration due to gravity IS 0 so time period will be infinite