Answer : The heat required is, 7200 calories.
Explanation :
The process involved in this problem are :
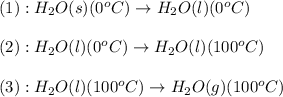
The expression used will be:
![\Delta H=m* \Delta H_(fusion)+[m* c_(p,l)* (T_(final)-T_(initial))]+m* \Delta H_(vap)](https://img.qammunity.org/2021/formulas/chemistry/high-school/bc324qx8jas3k8swtybtdjpadx6g7aji32.png)
where,
m = mass of ice = 10.0 g
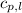 = specific heat of liquid water =
= specific heat of liquid water =
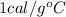
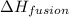 = enthalpy change for fusion =
= enthalpy change for fusion =
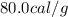
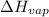 = enthalpy change for vaporization =
= enthalpy change for vaporization =
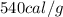
Now put all the given values in the above expression, we get:
![\Delta H=10.0g* 80.0cal/g+[10.0g* 1cal/g^oC* (100-0)^oC]+10.0g* 540cal/g](https://img.qammunity.org/2021/formulas/chemistry/high-school/4e4zkbasyc3cta2fdf9meq7x4yyaq8lrxo.png)
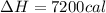
Therefore, the heat required is, 7200 calories.