Question

(a) Suppose anxn has finite radius of convergence R and an ≥ 0 for all n. Show that if the series converges at R, then it also converges at −R.

(b) Give an example of a power series whose interval of convergence is exactly (−1, 1].

Answer 1

a) See the proof below.

b)
`\sum ((-x)^n)/(n)`

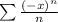
Explanation:

Part a

For this case we assume that we have the following series
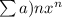`\sum a)n x^n` and this series has a finite radius of convergence
`R <\infty` and we assume that
`a_n \geq 0` for all n, this information is given by the problem.

We assume that the series converges at the point
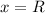`x= R` since w eknwo that converges, and since converges we can conclude that:

`\sum a)n R^n < \infty`

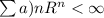
For this case we need to show that converges also for
`x=-R`

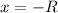
So we need to proof that
`\sum a_n (-R)^n < \infty`

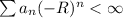
We can do some algebra and we can rewrite the following expression like this:

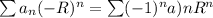`\sum a_n (-R)^n = \sum (-1)^n a)n R^n` and we see that the last series is alternating.

Since we know that
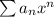`\sum a_n x^n` converges then the sequence {
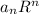`a_n R^n`} must be positive and we need to have
`lim_(n\to \infty) a^n R^n = 0`

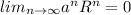
And then by the alternating series test we can conclude that
`\sum a_n (-R)^n` also converges. And then we conclude that the power series
`a_n x^n` converges for
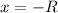`x=-R` ,and that complete the proof.

Part b

For this case we need to provide a series whose interval of convergence is exactly (-1,1]

And the best function for this
`((-x)^n)/(n)`

Because the series
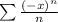`\sum ((-x)^n)/(n)` converges to
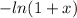`-ln(1+x)` when
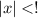`|x|<!` using the root test.

But by the properties of the natural log the series diverges at
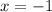`x=-1` because
`\sum (1)/(n) =\infty` and for
`x=1` we know that converges since
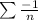`\sum (-1)/(n)` is an alternating series that converges because the expression tends to 0.