Question

A 25,000-kg train car moving at 2.50 m/s collides with and connects to a train car of equal mass moving in the same direction at 1.00 m/s.

a. What is the speed of the connected cars?
b. How much does the kinetic energy of the system decrease during the collision?

Answer 1

a) 1.75m/s

b) 14,062.5J

Step-by-step explanation:

• a) We solve this problem using linear momentum

`p=mv`

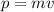
where
`p` is the momentum,
`m` is the mass, and
`v` is the velocity.

the momentum of the first train before the collision:

`p_(1)=m_(1)v_(1)`

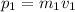
where
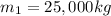`m_(1)=25,000kg` and
`v_(1)=2.5m/s`

`p_(1)=(25,000kg)(2.5m/s)`

`p_(1)=62,500kgm/s`

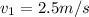
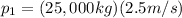
the momentum of the second train before the collision:

`p_(2)=m_(2)v_(2)`

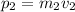
where
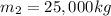`m_(2)=25,000kg` and
`v_(1)=1m/s`

`p_(2)=(25,000kg)(1m/s)`

`p_(2)=25,000kgm/s`

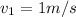
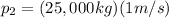
the total momentum before the collision is:

`p_(1)+p_(2)`

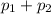
and due to the conservation of linear momentum: the amount of linear momentum before the collision must be the same after the collision.

so due to conservation:

`p_(1)+p_(2)=p_(f)`

the linear momentum of the two train system after the collision

`p_(f)=m_(f)v_(f)`

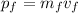
where
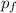`p_(f)` is the final linear momentum,
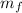`m_(f)` is the final mass of the system, if the two cars end up connected the mass is:

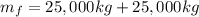`m_(f)=25,000kg+25,000kg` (the sum of the mass of the two cars)

`m_(f)=50,000kg`

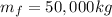
and
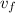`v_(f)` is the final speed: the speed of the connected cars.

so, going back to the conservation of momentum

`p_(1)+p_(2)=m_(f)v_(f)`

replacing all known values:

`87,500kgm/s=(50,000kg)v_(f)`

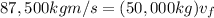
clearing for the final speed:

`v_(f)=(87,500kgm/s)/(50,000kg) =1.75m/s`

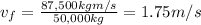
• b) the initial kinetic energy:

`k1+k2`

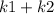
which is:

`(1)/(2) m_(1)v_(1)^2+(1)/(2) m_(2)v_(2)`

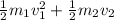
replacing all known values:

`(1)/(2)(25,000kg)(2.5m/s)^2+(1)/(2)(25,000kg)(1m/s)^2\\=(1)/(2)(25,000kg)(6.25m^2/s^2)+(1)/(2)(25,000kg)(1m^2/s^2)\\=78,125J+12,500J\\=90,625J`

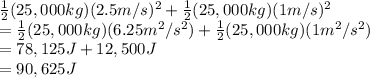
anf the final kinetic energy is:

`k_(f)=(1)/(2) m_(f)v_(f)^2\\k_(f)=(1)/(2) (50,000kg)(1.75m/s)^2\\k_(f)=(1)/(2) (50,000kg)(3.0625m^2/s^2)\\k_(f)=76,562.5J`

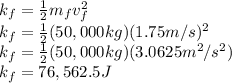
the difference is:

`90,625J-76,562.5J=14,062.5J`

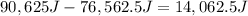
the kinetic energy of the system decreased 14,062.5J