Answer:
The angle is approximately
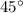 .
.
Explanation:
We should start with a diagram (like the one attached). Notice the length of the tower and the length of the shadow are the legs of a right triangle, and the angle of elevation is an acute angle of that triangle.
Since we are given the opposite and adjacent sides to the angle, we will use the tangent function:
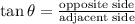
In this case, the opposite side is the height of the tower, 166 ft. The adjacent side is the length of the shadow, 167 ft. So, we have:
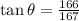
To get the angle, we need to use inverse tangent:

The angle is approximated
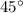 when rounded to the nearest degree.
when rounded to the nearest degree.