Question

A small, 300 g cart is moving at 1.20 m/s on an air track when it collides with a larger, 2.00 kg cart at rest?

After the collision, the small cart recoils at 0.810m/s
What is the speed of the large cart after collision?

Answer 1

The speed of the large cart after collision is 0.301 m/s.

Step-by-step explanation:

Given that,

Mass of the cart,
`m_1 = 300\ g = 0.3\ kg`

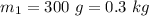
Initial speed of the cart,
`u_1=1.2\ m/s`

Mass of the larger cart,
`m_2 = 2\ kg`

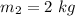
Initial speed of the larger cart,
`u_2=0`

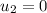
After the collision,

Final speed of the smaller cart,
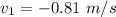`v_1=-0.81\ m/s` (as its recolis)

To find,

The speed of the large cart after collision.

Solution,

Let
`v_2` is the speed of the large cart after collision. It can be calculated using conservation of momentum as :

`m_1u_1+m_2u_2=m_1v_1+m_2v_2`

`m_1u_1+m_2u_2-m_1v_1=m_2v_2`

`v_2=(m_1u_1+m_2u_2-m_1v_1)/(m_2)`

`v_2=(0.3* 1.2+0-0.3* (-0.81))/(2)`

`v_2=0.301\ m/s`

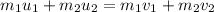
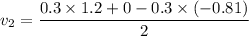
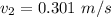
So, the speed of the large cart after collision is 0.301 m/s.