Answer:
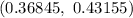
Explanation:
Let p be the population proportion of readers who would like more coverage of local news.
As per given , we have
sample size :=1600
sample proportion :
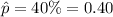
The confidence interval for population proportion is given by :-
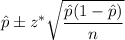
From z-table ,
For 99% confidence interval the z-value is 2.576.
Substitute all the values in the above formula , we get
The 99% confidence interval for the proportion of readers who would like more coverage of local news as
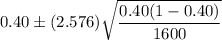
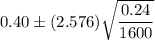
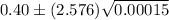
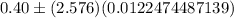
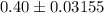
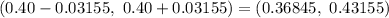
Hence, the 99% confidence interval for the proportion of readers who would like more coverage of local news is
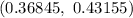 .
.