Question

AJ graphs the function f(x)=-(x+2)^(2)-1

part 1 : What mistake did AJ make in the graph?
part 2: Evaluate any two x-values (between -5 and 5) into AJ's function. Show your work. How does your work prove that AJ made a mistake in the graph?

Answer 1

Part 1: AJ reflected over x-axis.

Part 2:
`(0,-5)` and
`(-1,-2)`

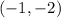
AJ plotted the graph using the function
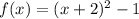`f(x)=(x+2)^(2)-1` . This resulted the graph to reflect over x-axis

Explanation:

Part 1: AJ mistakenly plotted over x-axis, which means he reflected the graph over x-axis.The x-value remains the same. Only the y-values are transformed into its opposite sign.

Part 2:

Step 1: Plotting any two values for the function
`f(x)=-(x+2)^(2)-1`

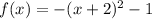
Substituting x=0, we get,

`\begin{aligned}y=f(0) &=-(0+2)^(2)-1 \\=&-(2)^(2)-1 \\=&-4-1=-5 \\& y=-5\end{aligned}`

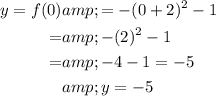
Substituting x=-1, we get,

`\begin{aligned}y=f(-1) &=-(-1+2)^(2)-1 \\=&-(1)^(2)-1 \\=&-1-1=-2 \\& y=-2\end{aligned}`

The two x-values for AJ’s function is
`(0,-5)` and
`(-1,-2)`

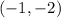
Step 2:

AJ plotted the graph using the function
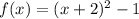`f(x)=(x+2)^(2)-1` . This resulted the graph to reflect over x-axis.