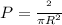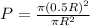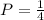Question

A point is selected at random inside a circle. Find the probability that the point is closer to the center of the circle than to its circumference.

Answer 1

Answer:0.25

Explanation:

Suppose a circle of Radius R

Points which are near to the circle will lie in the vicinity of center up to a distance r

r should be equal to
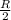`(R)/(2)` i.e. beyond 0.5 R points are away from the center and inside 0.5 R it is closer to center

Probability of finding a point closer to the circle is

`P=(\pir^2)/(\pi R^2)`

`P=(\pi (0.5R)^2)/(\pi R^2)`

`P=(1)/(4)`