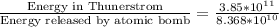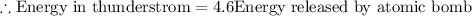Question

The energy of a thunderstorm results from the condensation of water vapor in humid air. Suppose a thunderstorm could condense all the water vapor in 10 km3 of air. How much heat does this release? (You may assume each cubic meter of air contains 0.017 kg of water vapor.) How does this compare to an atomic bomb which releases an energy of 2 x 1010 kcal?

Answer 1

To solve this problem we will define the values given for the latent heat required by condensation the net mass of water and apply the concept of heat released. Later we will compare the two values.

Latent heat required for condensation is

`L_c = 2264KJ/Kg`

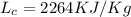
Air contain water:

`m = 10*1000^3*0.017`

`m = 1.7*10^8kg`

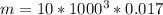
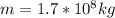
Now the heat released is

`Q = mL_c`

`Q = (1.7*10^8)(2264.7)`

`Q = 3.85*10^(11)KJ`

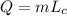
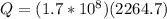
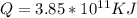
Using the value of energy released by atomic bomb, which is
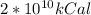`2*10^(10)kCal` and converting in Jules,

`E = 2*10^(10)kCal((4.184KJ)/(1kCal))`

`E = 8.368*10^(10)KJ`

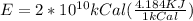
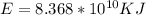
Compariong we have that,

`\frac{\text{Energy in Thunerstrom}}{\text{Energy released by atomic bomb}} = (3.85*10^(11))/(8.368*10^(10))`

`\therefore \text{Energy in thunderstrom} = 4.6 \text{Energy released by atomic bomb}`