Answer:
120 distinct results are possible if no child is to receive more than one gifts.
Explanation:
When the order is not important, we use the combination formula:
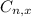 is the number of different combinatios of x objects from a set of n elements, given by the following formula.
is the number of different combinatios of x objects from a set of n elements, given by the following formula.
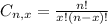
The order is said to be not important if for example, John receiving the Buffalo Bills jersey and then Laura receiving the Cleveland Browns jersey is the same as Laura receiving the Cleveland Browns jersey before John receives the Buffalo Bills jersey.
In this problem, we have that:
Combinations of 7 from a set of 10 elements. So
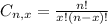
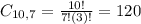
120 distinct results are possible if no child is to receive more than one gifts.