Question

What is the significance of the mean of a probability​ distribution?

Answer 1

See explanation below.

Explanation:

If we have a continuous variable the expected value is defined as:

`E(X) = \mu = \int_(a)^b x f(x) dx`

Where a and b are the limits for the distribution and
`f(x)` represent the density function.

If we have a discrete random variable X, the expected value is defined as:

`E(X) = \sum_(i=1)^n x_i P(X_i)`

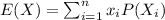
The mean is the most common measure of central tendency in order to describe a probability distribution.

The expected value also represent the first central moment of the random variable defined as:

`\mu_1= E[(X-E[X])^1] =\int_(-\infty)^(\infty) (x-\mu)^n f(x) dx`

If we assum that X is a continuous random variable.