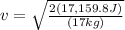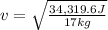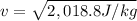Answer:
a)

b)
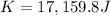
c)

Step-by-step explanation:
The information we have is
mass:
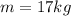
height:
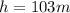
and we also know the acceleration of gravity is:

a) the potential energy is:
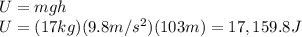
b) let's call the potential energy at the top of the cliff
 and at the bottom
and at the bottom
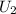 , and call the kinetic energy at the top of the cliff
, and call the kinetic energy at the top of the cliff
 and at the bottom of the cliff
and at the bottom of the cliff
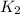 . The law of conservation of energy tells us that:
. The law of conservation of energy tells us that:
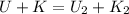
and because at the top of the cliff the rock does not move the kinetic energy there is zero.
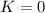 . In addition, when reaching the bottom of the cliff the height is
. In addition, when reaching the bottom of the cliff the height is
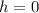 , so that the potential energy at the bottom is zero:
, so that the potential energy at the bottom is zero:
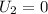
so:

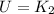
The kinetic energy when the stone touches the ground is the same as the potential energy at the top of the cliff:
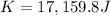
c) to find the speed we will use the formula for kinetic energy
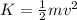
clearing for the speed:

and we already know the kinetic energy as the rock strikes the ground:
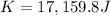
so the speed: