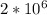Answer:
Processor P_2 is faster than P_1.
Part A:
For Processor P_1:
CPI=2.6
For Processor P_2:
CPI=2
Part B:
For Processor P_1:
CPU CLOCK CYClE=

For Processor P_2:
CPU CLOCK CYClE=
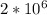
Step-by-step explanation:
We will find the instructions executed of each class:
For Class A=1*10^{6} *10%=1*10^{5}
For Class B=1*10^{6} *20%=2*10^{5}
For Class C=1*10^{6} *50%=5*10^{5}
For Class D=1*10^{6} *20%=2*10^{5}
CPU CLOCK CYClE=
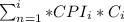
Where:
C_i is the instructions of each class (Calculated above)
For Processor P_1:
CPU CLOCK CYClE=

CPU CLOCK CYClE=

For Processor P_2:
CPU CLOCK CYClE=
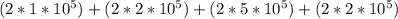
CPU CLOCK CYClE=
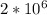
Now:
CPU TIME=CPU CLOCK CYClE/CYCLE RATE
For Processor P_1:
CPU TIME=
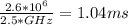
For Processor P_2:
CPU TIME=

Processor P_2 is faster than P_1.
Part A:
CPI=CPU CLOCK CYClE/Number of instructions
For Processor P_1:
CPI=
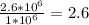
For Processor P_2:
CPI=
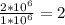
Part B:
For Processor P_1:
CPU CLOCK CYClE=

CPU CLOCK CYClE=

For Processor P_2:
CPU CLOCK CYClE=
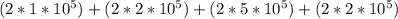
CPU CLOCK CYClE=