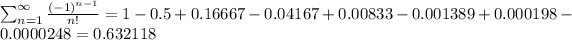Answer:
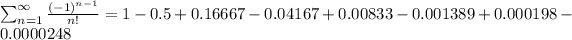
For the 7th term we have 3 decimals of approximation but our value is 0.000198 higher than the error required, so we can use the 8th term and we have that
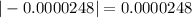 and with this we have 4 decimals of approximation so if we add the first 8 terms we have a good approximation for the series with an error bound lower than 0.0001.
and with this we have 4 decimals of approximation so if we add the first 8 terms we have a good approximation for the series with an error bound lower than 0.0001.
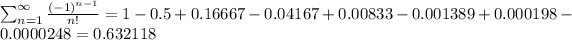
Explanation:
Assuming the following series:
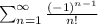
We want to approximate the value for the series with less than 0.0001 of error.
First we need to ensure that the series converges. If we have a series
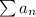 where
where
 [/tex] or
[/tex] or
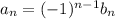 where
where
 for all n if we satisfy the two conditions given:
for all n if we satisfy the two conditions given:
1)
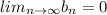
2) {
 } is a decreasing sequence
} is a decreasing sequence
Then
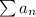 is convergent. For this case we have that:
is convergent. For this case we have that:
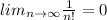
And
 because
because
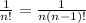 and
and

So then we satisfy both conditions and then the series converges. Now in order to find the approximation with the error required we can write the first terms for the series like this:
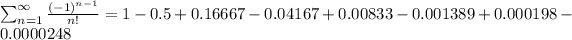
For the 7th term we have 3 decimals of approximation but our value is 0.000198 higher than the error required, so we can use the 8th term and we have that
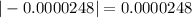 and with this we have 4 decimals of approximation so if we add the first 8 terms we have a good approximation for the series with an error bound lower than 0.0001.
and with this we have 4 decimals of approximation so if we add the first 8 terms we have a good approximation for the series with an error bound lower than 0.0001.