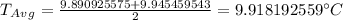Answer:
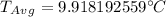
Step-by-step explanation:
The problem tell us that the temperature as function of time in downtown mathville is given by:
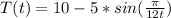
The average temperature over a given interval can be calculated as:
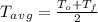
Where:
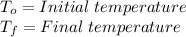
So, the initial temperature in this case, would be the temperature at noon, and the final temperature would be the temperature at midnight:
Therefore:
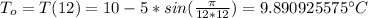
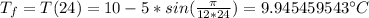
Hence, the average temperature between noon and midnight is: