Question

For a normal distribution with μ=500 and σ=100, what is the minimum score necessary to be in the top 60% of the distribution?

Answer 1

475.

Explanation:

We have been given that for a normal distribution with μ=500 and σ=100. We are asked to find the minimum score that is necessary to be in the top 60% of the distribution.

We will use z-score formula and normal distribution table to solve our given problem.

`z=(x-\mu)/(\sigma)`

Top 60% means greater than 40%.

Let us find z-score corresponding to normal score to 40% or 0.40.

Using normal distribution table, we got a z-score of
`-0.25`.

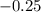Upon substituting our given values in z-score formula, we will get:

`-0.25=(x-500)/(100)`

`-0.25*100=(x-500)/(100)*100`

`-25=x-500`

`-25+500=x-500+500`

`x=475`

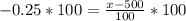
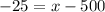
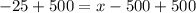
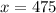
Therefore, the minimum score necessary to be in the top 60% of the distribution is 475.