Question

It has been established that under normal environmental conditions, adult largemouth bass in Silver Lake have an average length of 12.3 inches with a standard deviation of 3 inches. People who have been fishing Silver Lake for some time claim that this year they are catching smaller than usual largemouth bass. A research group from the Department of Natural Resources took a random sample of 100 adult largemouth bass from Silver Lake and found the mean of this sample to be 11.2 inches. Which of the following is the most appropriate statistical conclusion?

1. The researchers cannot conclude that the fish are smaller than what is normal because 11.2 inches is less than one standard deviation from the established mean (12.3 inches) for this species.

2. The researchers can conclude that the fish are smaller than what is normal because the sample mean should be almost identical to the population mean with a large sample of 100 fish.

3. The researchers can conclude that the fish are smaller than what is normal because the difference between 12.3 inches and 11.2 inches is much larger than the expected sampling erro.

Answer 1

Option 3. The researchers can conclude that the fish are smaller than what is normal because the difference between 12.3 inches and 11.2 inches is much larger than the expected sampling error.

Explanation:

We are given the following in the question:

Population mean, μ = 12.3 inches

Sample mean,
`\bar{x}` = 11.2 inches

Sample size, n = 100

Alpha, α = 0.05

Population standard deviation, σ = 3 inches

First, we design the null and the alternate hypothesis

`H_(0): \mu = 12.3\text{ inches}\\H_A: \mu < 12.3\text{ inches}`

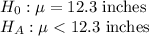
We use one-tailed z test to perform this hypothesis.

Formula:

`z_(stat) = \displaystyle\frac{\bar{x} - \mu}{(\sigma)/(√(n)) }`

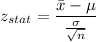
Putting all the values, we have

`z_(stat) = \displaystyle(11.2 -12.3)/((3)/(√(100)) ) = -3.67`

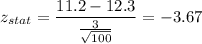
Now,
`z_(critical) \text{ at 0.05 level of significance } = -1.64`

Since,

`z_(stat) < z_(critical)`

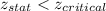
We reject the null hypothesis and accept the alternate hypothesis.

Thus, we conclude that this year they are catching smaller than usual largemouth bass.

Option 3. The researchers can conclude that the fish are smaller than what is normal because the difference between 12.3 inches and 11.2 inches is much larger than the expected sampling error.