Answer:
Option C) 0.0602
Explanation:
We are given the following in the question:
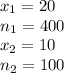
Let p1 and p2 be the proportion of all parts from suppliers 1 and 2, respectively, that are defective.
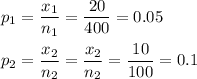
First, we design the null and the alternate hypothesis
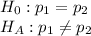
We use Two-tailed z test to perform this hypothesis.
Formula:
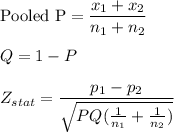
Putting all the values, we get,
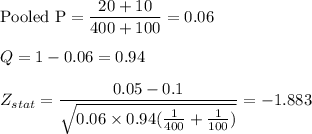
Now, we calculate the p-value from the table at 0.05 significance level.
P-value = 0.0602
Thus, the correct answer is
Option C) 0.0602