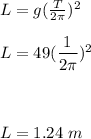Answer:
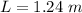
Step-by-step explanation:
It is known that the oscillation period of a pendulum can be described as
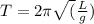 ,
,
where T is the oscillation period, L is the length of the pendulum and, g is the gravity.
Solving For the length we get:
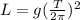 .
.
We know that g equals 5 times earth's gravity,
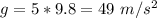 ,
,
and from the angular displacement graphics, it can be seen that the period is
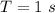 .
.
Now, we can easily compute the length of the pendulum: