Answer:
A. 4 (RootIndex 3 StartRoot 7 x EndRoot) or
![4(\sqrt[3]{7x})](https://img.qammunity.org/2021/formulas/mathematics/middle-school/4m9nzae0dcfab5wrhpsno4a8l459f1bfnt.png)
Explanation:
Given:
A radical whose value is,
![r_1=\sqrt[3]{7x}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/rn3b469s7jezxcob2jpuf5y94v91amuedv.png)
Now, we need to find the like radical for
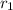 .
.
Let the like radical be
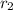 .
.
As per the definition of like radicals, like radicals are those that can be expressed as multiples of each other.
So, if two radicals
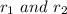 are like radicals, then
are like radicals, then
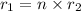
Where, 'n' is a real number.
Here,
![r_1=\sqrt[3]{7x}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/rn3b469s7jezxcob2jpuf5y94v91amuedv.png)
Now, let us check all the options .
Option A:
4 (RootIndex 3 StartRoot 7 x EndRoot) or
![r_2=4\sqrt[3]{7x}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/7z8i3z7nrqarw069qk0ml08hi186y8ljs2.png)
Now, we observe that
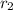 is a multiple of
is a multiple of
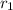 because
because
![r_2=4* \sqrt[3]{7x}\\\\ r_2=4* r_1..............(r_1=\sqrt[3]{7x})](https://img.qammunity.org/2021/formulas/mathematics/middle-school/s4xkb2o0pwvibx28fxraqyq8ex1oujgyra.png)
Therefore, option A is correct.
Option B:
StartRoot 7 x EndRoot or
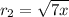
As the above radical is square root and not a cubic root, this option is incorrect.
Option C:
x (RootIndex 3 StartRoot 7 EndRoot) or
![r_2=x\sqrt[3]{7}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/jqu4p87cfjxnyf1d0busryfj8zfrij4e5i.png)
As the term inside the cubic root is not same as that of
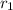 , this option is also incorrect.
, this option is also incorrect.
Option D:
7 StartRoot x EndRoot or
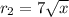
As the above radical is square root and not a cubic root, this option is incorrect.
Therefore, the like radical is option (A) only.