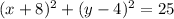Question

A cell tower is located at and transmits a circular signal that covers three major cities. The three cities are located on the circle and have the following coordinates: , , and . Find the equation of the circle.

Answer 1

`(x+8)^2 +(y-4)^2 = 25`

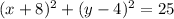
Explanation:

Assuming this complete problem: "A cell tower is located at (-8, 4) and transmits a circular signal that covers three major cities. The three cities are located on the circle and have the following coordinates: G (-4, 7), H (-13, 4), and I (-8, -1). Find the equation of the circle"

For this case the generla equation for the circle is given by:

`(x-h)^2 +(y-k)^2 = r^2`

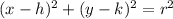
From the info we know that the tower is located at (-8, 4) so then h = -8 and k = 4, so then we need to find the radius. So we have the equation like this:
`(x+8)^2 +(y-4)^2 = r^2`

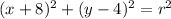
If the 3 points are on the circle then satisfy the equation. We can use the first point (-4,7) and if we replace we can find the value for
`r^2`

`(-4+8)^2 +(7-4)^2 =25= r^2`

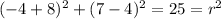
So then
`r = √(25)=5`

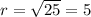
And if we replace the second point we got this:

`(-13+8)^2 +(4-4)^2 = 25 =r^2`

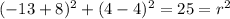
And for the third point we have:

`(-8+8)^2 +(-1-4)^2 = 25 =r^2`

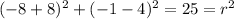
And we got the same result.

So then our final equation is given:

`(x+8)^2 +(y-4)^2 = 25`