Question

Consider the function f(x) = 4x - x². Find the average rate of change over the given time intervals. 0.5 <= x <= 1, average rate of change =?

Answer 1

your trash kid

Explanation:

Answer 2

`\text{Average rate of change}=2.50`

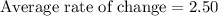
Explanation:

We have been given a function
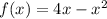`f(x)=4x-x^2`. We are asked to find average rate of change over the given time intervals of
`0.5\leq x\leq 1`.

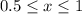We will average rate change formula to solve our given problem.

`\text{Average rate of change}=(f(b)-f(a))/(b-a)`

`\text{Average rate of change}=(f(1)-f(0.5))/(1-0.5)`

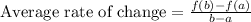
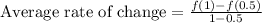
Let us find f(1) and f(0.5) using our given function.

`f(1)=4(1)-(1)^2`

`f(1)=4-1`

`f(1)=3`

`f(0.5)=4(0.5)-(0.5)^2`

`f(0.5)=2-0.25`

`f(0.5)=1.75`

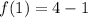
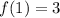
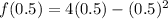
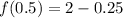
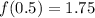
Upon substituting these values in average rate of change formula, we will get:

`\text{Average rate of change}=(3-1.75)/(1-0.5)`

`\text{Average rate of change}=(1.25)/(0.5)`

`\text{Average rate of change}=2.50`

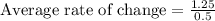
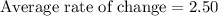
Therefore, the average rate of change over the interval
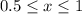`0.5\leq x\leq 1` would be 2.50.