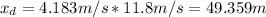Answer:
a)
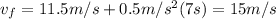
b)

c)
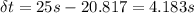
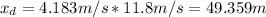
Step-by-step explanation:
For this case we have the following data given:
 represent the initial velocity
represent the initial velocity
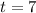 the time when we have acceleration
the time when we have acceleration
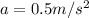 the acceleration
the acceleration
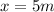 represent the distance
represent the distance
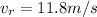 the velocity for the second place winner
the velocity for the second place winner
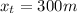 represent the total distance
represent the total distance
Part a
For this case we can use the following equation:
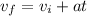
And if we replace we got:
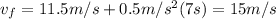
Part b
For this case first let's calculate the time taken to end the race with the initial velocity provided
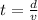 , and if we replace we got:
, and if we replace we got:
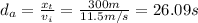
Now we can find the distance covered whn she accelerates
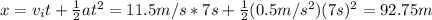
Now we can calculate the distance for the final velocity:
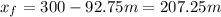
And the time to complet this distance is:
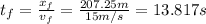
And the total time would be then:
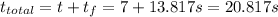
And we can calculate the tame saved taking the difference from the total tim and

Part c
For this case we have the velocity for the second player;
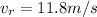
The total distanc for this case woudl be 300--5 = 295 m we can calculate the time to travel this distance at 11.8 m/s like this:
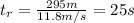
And if we find the difference between this time and the
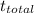 we got:
we got:
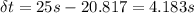
And the distance would be: